I needed a map editor with more features than what I saw included in TILED back in August, so I decided to try my own hand at creating a map editor. It’s just an interactive grid, right? Not quite. At least in the approach I took.

I started writing the tile editor with C++ and SDL. Implementing drag functionality was pretty easy since that was baked in the SDL API, however, I didn’t want to build the UI widgets from scratch. Unfortunately, the existing UIs I found weren’t compatible with SDL, so I had to pivot and use straight OpenGL and matrix math.

Because I was ditching the SDL framework, I had to implement my own drag logic, which is what I will discuss in this post.

Moving Objects with Mouse Picking

I needed the ability to select objects in 3D space, which lead me to a technique called mouse picking. This technique utilizes ray casting, which is how you detect if a line (a ray) intersects with something else.

The article “Mouse Picking with Ray Casting” by Anton Gerdelan helped explain the different planes/spaces and what they represented.

In order to move the objects in 3D space at a distance that matched the mouse movement, I had to transform the coordinates between screen and world spaces. When working with 3D coordinates, there are several spaces or planes that have their own coordinates.

A very simplified list of these spaces are:
Screen Space > Projection (Eye) Space > World Space > Model Space.

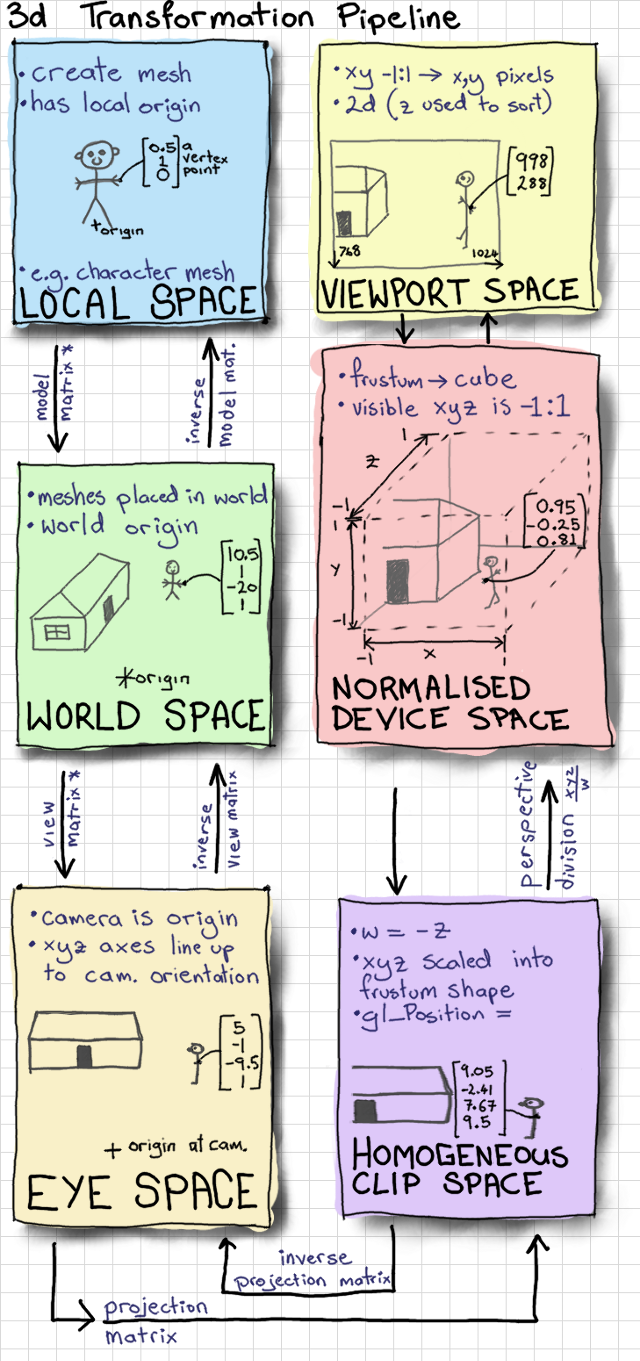
Fully understanding the transformation formula was a challenge for me. Normalization and calculating the inverse Projection Matrix tripped me up due to a combination of confusion and erroneous input.

The Solution

Here are some code examples of the final working solution.

Initialization of Projection, View, Model

Projection = glm::perspective(1.0f, 4.0f / 3.0f, 1.0f, 1024.1f);
GlobalProjection = Projection;

CameraDistance = 10.0f;
GlobalCameraDistance = CameraDistance;

View = glm::lookAt(
glm::vec3(0, 0, CameraDistance), // Camera location
glm::vec3(0, 0, 0), // Where camera is looking
glm::vec3(0, 1, 0) // Camera head is facing up
);
GlobalView = View;

Model = glm::mat4(1.0f);
GlobalModel = Model;

MVP = Projection * View * Model; // Matrix multiplication

View to World Coordinate Transformation

// SCREEN SPACE: mouse_x and mouse_y are screen space
glm::vec3 Application::viewToWorldCoordTransform(int mouse_x, int mouse_y) {
    // NORMALISED DEVICE SPACE
    double x = 2.0 * mouse_x / WINDOW_WIDTH - 1;
    double y = 2.0 * mouse_y / WINDOW_HEIGHT - 1;

    // HOMOGENEOUS SPACE
    glm::vec4 screenPos = glm::vec4(x, -y, -1.0f, 1.0f);

    // Projection/Eye Space
    glm::mat4 ProjectView = GlobalProjection * GlobalView;
    glm::mat4 viewProjectionInverse = inverse(ProjectView);

    glm::vec4 worldPos = viewProjectionInverse * screenPos;
    return glm::vec3(worldPos);
}

At first this algorithm felt a bit magical to me. There were things going on I wasn’t entirely wrapping my head around, and when I stepped through the algorithm I got lost at the inverse matrix multiplication. In addition, the “Mouse Picking” article normalizes the world space values, which we don’t need.

The algorithm requires an understanding of matrix math and how normalization works. I wasted some time working on a loose understanding, which resulted in introducing more errors and second guessing myself as I tried to locate the error in my calculations. A couple times I resorted to manually calculating the transformations on paper.

The Fourth Component
When working with transformation, the W component is meant to represent if the vector is directional (W=0) or positional (W=1). In my tinkering, I made the mistake of setting incorrect values for that fourth component.

Mouse cursor vs Clicked Object
Another point of confusion was assuming the depth of the object would be calculated from the above conversion function. The function above is converting the coords for the mouse pointer, which exists at the projection depth, not the object that is being clicked. This is important, because the X and Y coords change as the depth changes due to how perspective works.

// Tiles = Array of objects representing a single tile with x,y,z floats
// CameraDistance is a float representing the distance of camera from origin

Tiles[0]._x = static_cast<float>(delta_transformed2.x) * CameraDistance;
Tiles[0]._y = static_cast<float>(delta_transformed2.y) * CameraDistance;
Model = glm::translate(glm::mat4(1.0f), glm::vec3(transform.x, transform.y, 0));

Summary

In order to drag an object in 3D space there needs to be some type of translation between the screen view and the world view so the coords can be transformed.

Doing the transformation yourself isn’t always required, some frameworks do this for you, and the matrix math is hidden away. However, understanding the concepts and what is happening in the background is good to know. For example, Unity has local and world coords, as well as raycasting functions.

By the time I figured out the transform problem (which was a while due to getting distracted) Tiled came out with some features that actually addressed part of my original problem. In addition, it is now open sourced, open for collaboration, and uses the QT framework. Given I have the time, I will be focusing my efforts on contributing to Tiled instead of rolling my own.